Pertemuan ke-4


Dalam pertemuan kali ini, kami diajarkan mengenai "Introduction to Tree, Binary Tree and Expression Tree".

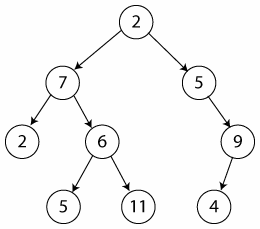
Tree : adalah koleksi dari 1 atau lebih node. (seperti yang di tunjukan dalam gambar).

Note : Dalam tree ada yang disebut sebagai root dan ada juga yg disebut sebagai leave.

Root : Adalah node yang berada pada yang paling atas atau yang paling utama. Dalam contoh gambar berikut, rootnya adalah 2.

Leaf : Adalah node yang berada pada yang paling bawah dimana ia sudah tidak beranak cucu atau memilik cabang lagi. Leave pada gambar berikut adalah 2,5,11 dan 4.

Ada juga yang disebut dengan Level. Dimana setiap Tingkat memiliki level tertentu apa bila berada dalam baris yg sama. Contohnya:

• Level 1 : 2 (karena berada dalam baris pertama dan di baris tsb hanya ada angka 2).
• Level 2 : 7 dan 5.
• Level 3 : 2 , 6, dan 9.
• Level 4 : 5, 11, dan 4.

Tree juga sering disebut seperti silsilah keluarga, contohnya Orangtua (Parent) dari angka 7 dan 5 adalah 2. Anak (Child) dari angka 6 adalah 5 dan 11, dan seterusnya.

Binary Tree :
Binary Tree adalah struktur dari Tree yang setiap nodenya hanya boleh memiliki kurang dari 2 anak dari rootnya sampai leaf. Biasanya 2 anak cabang tersebut dibedakan menjadi bagian kiri dan bagian kanan.

Tipe Tipe Binary Tree:

• Perfect Binary Tree : Setiap bagian dari tree tsb memiliki depth yang sama. 

•  Complete Binary Tree : Setiap bagian memiliki depth yg sama kecuali pada bagian akhir akan ada kosong 1 node.

• Skewed Binary : adalah Binary yang setiap bagiannya hanya memiliki 1 anak saja.
• Balanced Binary Tree : Balanced ("seimbang") maka setiap bagian node dari binary tree tsb memiliki nilai maksimum node lebih besar 2^k dari level sebelumnya. 

Representasi dalam Binary Tree:

• Index Left Child adalah 2p + 1, dimana p adalah indeks parent.
• Index Right Child adalah 2p + 2.
• Index Parent adalah (p-1)/2.

Dalam Tree ada juga proses yang disebut sebagai prefix, postfix, dan infix.
Prefix : adalah bentuk equation dimana letak operator berada di depan.
Postfix : adalah bentuk equation dimana letak operator berada di belakang.
Infix : adalah bentuk equation dimana letak operator berada di tengah.

Contoh : 2+a+b/2 * 3

    Prefix : + 2 + a * / b 2 3

    Profix : 2 a b 2 / 3 * + + 

Contoh : a + (b/2) * 3 / 2

    Prefix : + a / * / b 2 3 2 

    Profix : a b 2 / 3 * 2 / +

*Note : (Seperti matematika dasar, operator bagi dilakukan lebih dahulu lalu  perkalian, lalu penjumlahan, apa bila ada parentheses () maka equation itu dihitung lebih dahulu).

Dimana:

• Infix : Left V Right.
• Prefix : V Left Right.
• Postfix Left Right V.

Tugas : C / A * 2 + 3 / 12 + 21
     Prefix : + + / * / C A 2 3 12 21 
     PostFix : C A 2 3 1 2 21 / * / + +


Nama : Dickson Saputra.
NIM : 1701291283

   www.binus.ac.id || www.skyconnectiva.com